Bias-Variance Trade-off는 Supervised learning에서 error를 처리할 때 중요하게 생각해야 하는 요소이다.
모델을 학습시킬 때, 우리의 목표는 bias와 variance가 모두 최소화되도록 하는 것이다. 그러나 일반적으로 bias와 variance는 동시에 최소화될 수 없는데, 이러한 현상을 bias-variance tradeoff라고 한다.
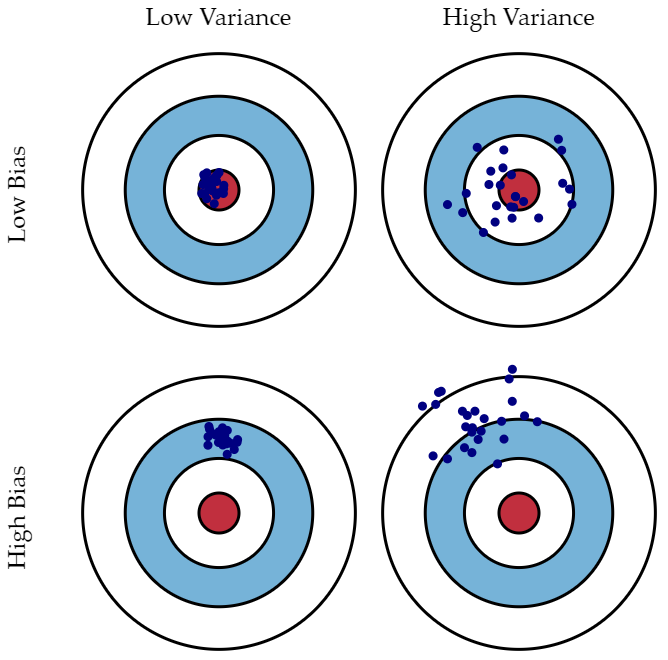
편향은 예측값이 정답과 얼마나 멀리 떨어져 있는지로 측정할 수 있고 분산은 예측값들끼리의 차이로 측정할 수 있다.
편향(Bias)
편향은 학습 알고리즘에서 잘못된 가정으로 인한 오류이다.
편향이 높으면 알고리즘이 feature(설명변수, 독립변수)와 target(종속변수)간의 관계를 놓칠 수 있고 이는 특성과 타겟변수의 관계를 잘 파악하지 못하기 때문에 under-fitting을 야기한다.
분산(Variance)
분산은 지나치게 복잡한 모델로 인한 error입니다. 훈련 데이터에 지나치게 적합시키려는 모델말입니다. 분산이 크면 과대 적합(Over-fitting)을 야기합니다. 분산이 큰 모델은 훈련 데이터에 지나치게 적합을 시켜 일반화가 되지 않은 모델입니다.
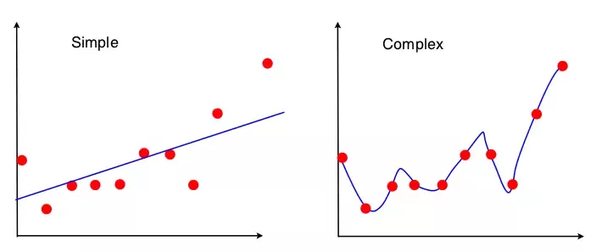
왼쪽은 큰 편향, 작은 분산 (high bias, low variance), 오른쪽은 작은 편향, 큰 분산 (low bias, high variance)를 나타낸다.
편향은 예측 값과 실제 값의 차이로 나타낼 수 있다. 왼쪽 그래프의 예측 값과 실제 값이 차이는 오른쪽 그래프보다 크다. 오른쪽 그래프의 예측 값과 실제 값의 차이는 0이고 이는 편향이 0이라는 뜻입니다.
분산은 왼쪽 그래프가 더 작다. 분산은 주어진 데이터로 학습한 모델이 예측한 값의 변동성을 뜻한다. 왼쪽 그래프는 일반화가 잘 되어 있기 때문에 예측 값이 일정한 패턴을 나타내지만 오른쪽 그래프는 들쑥날쑥하다. 이는 예측 값에 일정한 패턴이 없다는 뜻이다. 즉, 분산이 크다는 뜻이다.
편향-분산 Trade-off
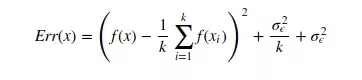
첫번째 term : 편향의 제곱
두 번째 term : 분산
세 번째 term : irreducible error
마지막 error는 일상생활에서 발생할 수 있는 불가피한 error를 뜻한다.
전체 모델의 error는 이렇게 편향, 분산, 불가피한 error를 모두 합한 것과 같다.
하지만 편향과 분산 간에는 trade-off 관계가 있다.
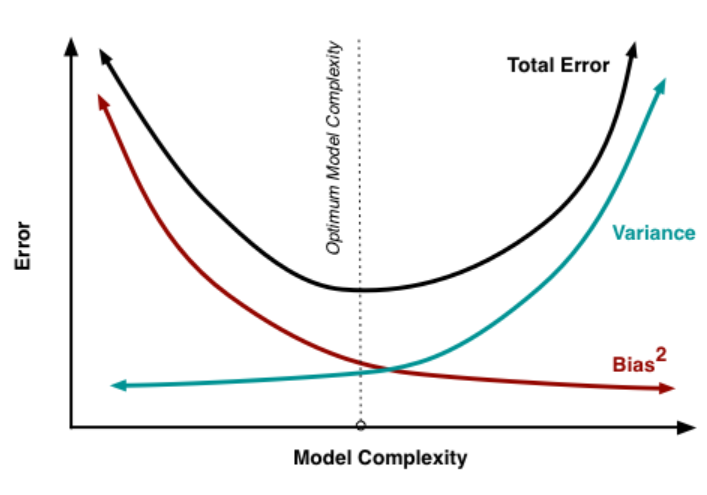
모델이 복잡할수록(high model complexity) bias는 감소하고 variance는 높아지며 (over-fitting이 발생할 가능성 높음)
모델이 간단할수록(low model complexity) bias는 증가하고 variance는 낮아진다. (under-fitting이 발생할 가능성 높음)
따라서 오류를 최소화하려면 편향과 분산의 합이 최소가 되는 적당한 지점을 찾아야 한다.
'Data Science > 데이터분석' 카테고리의 다른 글
| [기초통계학] 통계적 추정 (0) | 2022.06.16 |
|---|---|
| [기초통계학] 표본평균의 분포와 중심극한정리 (0) | 2022.06.16 |
| [기초통계학] 확률분포 (0) | 2022.06.16 |
| [기초통계학] 대표값 (0) | 2022.06.16 |
| [기초통계학] 자료의 분류 (0) | 2022.06.10 |
